はじめに：なぜ「変換」が重要なのか

スパースモデリングは，信号や画像から本質的な情報だけを抽出し，モデルを単純化するための強力なアプローチです．その代表的な手法である $ℓ_{1}$ 正則化（Lasso）は，データやモデルパラメータの多くの要素を直接ゼロにすることでスパース性を実現します．

しかし，私たちが扱う現実のデータ，例えば風景写真のピクセル値や音声波形などは，それ自体がスパース（多くの要素がゼロ）であることは稀です．このような密なデータに対して，より効果的にスパースモデリングを適用するにはどうすれば良いのでしょうか．

その答えの一つが，特徴空間におけるスパース正則化という考え方です．これは，データそのものではなく，何らかの 「変換」 を施した後の世界（特徴空間）でスパース性を仮定するアプローチです．

この考え方は，多くの成功した技術の根底にあります．

JPEG画像圧縮: 画像をピクセル単位ではなく，離散コサイン変換 (DCT) によって周波数成分に分解します．すると，多くの高周波成分（画像の細かい部分）はゼロに近くなるため，このスパース性を利用してデータを効率的に圧縮します．
音声認識: 音声波形をフーリエ変換によって周波数スペクトルに変換することで，音声の持つ特徴をより扱いやすい形で抽出できます．

このように，適切な「変換」は，データに内在する本質的な構造（スパース性）を顕在化させる役割を果たします．この記事では，この「特徴空間におけるスパース正則化」という枠組みに基づき，古典的な手法から最新の研究動向までを体系的に解説します．

一般的な問題設定：変換と正則化の組み合わせ

特徴空間におけるスパース正則化は，例えば以下の最適化問題として定式化できます．観測データ $y \in R^{K}$ から，未知の元信号 $x \in R^{N}$ を推定する問題を考えます．

x min \frac{1}{2} ∥ y - A x ∥_{2}^{2} + λ R (L x)

この式の各要素は以下の通りです．

$x \in R^{N}$ ：推定したい未知の信号や画像．
$A$ ：観測プロセスを表す行列（例：圧縮センシングにおける観測行列）．
$L$ ：信号 $x$ を特徴空間へ写すための線形変換．この選択が手法の特性を決定します．
$R (\cdot)$ ：変換後の特徴量 $L x$ に対してスパース性を課すための正則化関数．
$λ$ ：正則化の強さを制御するハイパーパラメータ．

この枠組みの利点は，変換 $L$ を柔軟に設計できる点にあり，これにより様々なデータの特性をモデル化することが可能になります．

多様な特徴空間：スパース性を探す場所

どのような「変換」と「正則化」の組み合わせがあるのか，具体的な事例を見ていきましょう．

1. 周波数成分のスパース性

変換 ( $L$ )：離散フーリエ変換 (DFT) や離散コサイン変換 (DCT)
正則化 ( $R$ )： $ℓ_{1}$ ノルムや混合 $ℓ_{2} / ℓ_{1}$ ノルム
応用先：音声信号処理，気象レーダー信号解析など

多くの自然信号は，時間領域では密な振幅を持ちますが，周波数領域に変換すると，エネルギーが特定の周波数に集中するスパースな構造を示すことがよくあります．

特に，気象レーダーの信号解析では，観測信号が特定の周波数帯域にまとまり（ブロック）を持つため，混合 $ℓ_{2} / ℓ_{1}$ ノルムを用いたブロックスパース正則化が有効です．ただし，どの周波数帯域にブロックが現れるかは観測対象によって変動するため，ブロック構造自体をデータから適応的に学習する LOP- $ℓ_{2} / ℓ_{1}$ のような手法が重要となります．LOP- $ℓ_{2} / ℓ_{1}$ に関する解説は最適なブロック構造を学習するブロックスパース正則化：LOP-l2l1 の紹介を参照ください．

2. 差分（エッジ）成分のスパース性

変換 ( $L$ )：差分作用素（隣接要素の差を計算する行列）
正則化 ( $R$ )： $ℓ_{1}$ ノルムや混合 $ℓ_{2} / ℓ_{1}$ ノルム
応用先：画像ノイズ除去，画像補完など

画像データは，「ほとんどの領域は滑らかで，値が急激に変化するのは物体の輪郭（エッジ）部分だけ」という強い構造を持っています．この性質に基づき，隣接ピクセル間の「差分」を取ると，エッジ以外の大部分はゼロに近くなります．この「差分信号のスパース性」を利用するのが，画像処理で広く用いられているTotal Variation (TV) 正則化です．

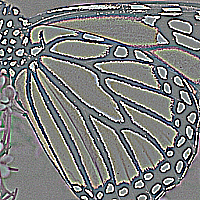
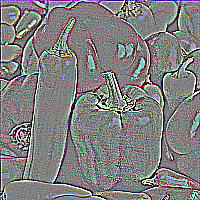
さらに，エッジは単にスパースであるだけでなく，エッジの方向や形状が揃っているという構造を持つことが多いです．これを捉えるために，混合 $ℓ_{2} / ℓ_{1}$ ノルムを用いるアプローチもあります．これは，エッジの方向ごとにグループ化し，各グループ内でのスパース性を強調するものです．また，エッジの場所や形状は画像ごとに異なるため，適応的なグループ化を行う LOP- $ℓ_{2} / ℓ_{1}$ のような手法が有効です．LOP- $ℓ_{2} / ℓ_{1}$ に関する解説は最適なブロック構造を学習するブロックスパース正則化：LOP-l2l1 の紹介を参照ください．

3. 特異値のスパース性（低ランク性）

変換 ( $L$ )：行列やテンソルの特異値を抽出する変換．行列の場合は，特異値分解 $X = U S V^{T}$ における $S$ の対角部分を，ベクトルとして構成する操作 $s = diag (S)$ に対応します．ただし，線形変換ではないため， $L$ を行列で表すことはできません．
正則化 ( $R$ )： $ℓ_{1}$ ノルム．特異値の $ℓ_{1}$ ノルムは 核ノルム（Nuclear Norm） と呼ばれます．
応用先：画像補完，画像ノイズ除去など

高次元のデータ（テンソル）には，しばしば「低ランク性」と呼ばれる構造が潜んでいます．これは直感的には，「データ全体が，実は少数の基本的なパターンの線形結合で表現できる」という性質です．この低ランク性は，行列・テンソルデータの特異値がスパースである（ごく少数の特異値だけが大きな値を持ち，残りはゼロに近い）ことと数学的に等価です．この性質を利用するのが，特異値の $ℓ_{1}$ ノルムである核ノルムを最小化するアプローチです．

4. 差分の特異値のスパース性（平滑性と低ランク性の融合）

変換 ( $L$ )：差分作用素
正則化 ( $R$ )：核ノルム
応用先：画像補完，画像ノイズ除去など

これは，2と3を組み合わせた，より発展的なアプローチです．「画像は滑らかである（差分がスパース）」という仮定に加え，「差分画像（エッジ画像）のパターン自体も，構造的で低ランクである」 と仮定します．これにより，単にエッジが少ないだけでなく，エッジの方向や形状が揃っているといった，より高度な画像の構造を捉えることが可能になります．Wangらの研究[4]で提案されたt-CTV（tensor Correlated Total Variation）は，この考え方に基づいています．

5. 差分の「学習された」変換後のスパース性（多層スパース性）

変換 ( $L$ )：差分作用素と，それに続く学習可能なユニタリ変換 $V$
正則化 ( $R$ )： $ℓ_{1}$ ノルムや再重み付き $ℓ_{1}$ ノルム（Log-sum Penalty）
応用先：画像補完など

これはさらに一歩進んだアプローチです．差分信号がスパースであることは認めつつ，「どのような基底でスパースになるか」を固定的な変換に頼るのではなく，データ自身から最適な基底 $V$ を学習します．Xueらの研究[3]で提案されたMLSTD（Multi-Layer Sparsity-based Tensor Decomposition）はこのアイデアを実現したもので，データに特化した変換を学習するため，より洗練されたスパース表現が得られます．

6. 深層展開による学習可能なフィルタ

変換 ( $L$ )：学習可能なフィルタ（例：時間方向のFIRフィルタ）
正則化 ( $R$ )：空間的な平滑性（グラフラプラシアン）など
応用先：時変グラフ信号の復元など

これまで紹介した手法が変換行列 $L$ を事前に設計するか，単一データから1つの変換を学習したのに対し，ここでは最適化アルゴリズム自体を深層学習の枠組みで「学習」させる 深層展開（Deep Unrolling） というアプローチを紹介します．

この手法の根幹にあるアイデアは，「最適化アルゴリズムをニューラルネットワークに見立てる」というものです．

最適化アルゴリズムを展開する：最急降下法やADMM (Alternating Direction Method of Multipliers) といった反復最適化アルゴリズムの各ステップを，ニューラルネットワークの1つの層として「展開（Unroll）」します．
パラメータを学習する：従来は人間が手で調整していたアルゴリズム内のハイパーパラメータ（例えば，正則化の強さやフィルタの係数）を，ネットワークの学習可能なパラメータと見なします．
End-to-Endで学習する：入力データと望ましい出力（正解データ）のペアを与え，バックプロパゲーションによって，これらのパラメータをデータセット全体で最適化します．

Kojimaらの研究[7]では，この深層展開の枠組みを時変グラフ信号の復元問題に適用しています．彼らの目的は，時間的にも空間的にも滑らかなグラフ信号を復元することです．ここで重要な役割を果たすのが，時間方向の滑らかさを捉える 差分フィルタ行列（差分作用素） $D$ です．従来手法では，このフィルタは[1, -1]のような単純な差分で固定されていました．しかし，Kojimaらの手法では，このフィルタの係数そのものを深層展開によって学習します．

その結果，単純な差分フィルタよりもデータの時間的な特性を巧みに捉える，より洗練されたフィルタが自動で獲得され，復元精度が向上します．このアプローチは，数理モデルにおける先見知識の解釈可能性を保ちつつ，データ駆動でその性能を最大限に引き出す，強力なパラダイムと言えるでしょう．

最適化手法：非可逆な変換への対処法

特徴空間でスパース性を考えると，最適化アルゴリズムの選択が重要になります．特に，変換 $L$ が非可逆 (non-invertible) である場合に課題が生じます．

離散コサイン変換やフーリエ変換のように逆変換が存在する可逆な変換であれば， $z = L x$ と変数変換し， $z$ について問題を解くことができます．しかし，差分作用素のように，変換の過程で情報が失われるため逆変換が一意に定まらない非可逆な変換では，この方法を直接適用することは困難です．

解決策：補助変数を用いた問題分解

この課題を解決する効果的な手法の一つが，ADMM (Alternating Direction Method of Multipliers) です．このアルゴリズムは，元の問題を扱いやすい複数のサブ問題に分解し，それらを協調させながら交互に解くことで，全体の最適解を探索します．

具体的には，元の問題を以下の等価な制約付き最適化問題に書き換えます．

x, z min \frac{1}{2} ∥ y - A x ∥_{2}^{2} + λ R (z) s.t. z = L x

ここで導入された補助変数 $z$ は，元の信号空間( $x$ )と特徴空間( $z$ )を仲介します．この定式化により，最適化問題を

$x$ に関する最小化（観測データへのフィッティング）
$z$ に関する最小化（特徴空間でのスパース化）

という，より単純な二つの部分問題に分離できます．ADMMなどのアルゴリズムは，この二つの部分問題を制約 $z = L x$ を満たしつつ交互に更新することで，全体の最適解を効率的に見つけ出します．さらに，各部分問題のソルバーが微分可能であれば，深層展開を用いて，正則化パラメータ $λ$ や変換行列 $L$ の係数を学習することも可能です．

まとめ

本記事では，「特徴空間におけるスパース正則化」という枠組みに基づき，信号や画像に潜む多様な構造を捉えるための様々なアプローチを解説しました．

キーポイント:

変換の選択が鍵：フーリエ変換，差分作用素，さらには学習可能な変換まで，適切な $L$ を選ぶことで，データの多様な側面を捉えられます．
正則化との組み合わせ： $ℓ_{1}$ ノルム，混合 $ℓ_{2} / ℓ_{1}$ ノルム，核ノルムなどを組み合わせることで，構造的な先見情報をモデルに組み込むことができます．
アルゴリズムの進化：ADMMや深層展開などの現代的な最適化手法により，非可逆な変換を含む複雑な問題も効率的に解けるようになりました．

以下の表は，本記事で紹介したアプローチをまとめたものです．

スパース性の対象	変換 $L$ の考え方	正則化 $R$ の考え方	主な応用・関連手法
周波数成分	周期的なパターンを抽出する	特定の周波数に集中する	周波数選択
差分（エッジ）	局所的な変化を捉える	変化点が少ない（滑らか）	Total Variation (TV) 正則化
特異値（低ランク性）	大域的な基本パターンを抽出する	パターンの種類が少ない	核ノルム正則化
差分の特異値	エッジのパターンに潜む構造を捉える	エッジのパターンが単純	t-CTV 正則化
差分の学習された基底	データに最適な基底を学習する	その基底で見たときにスパース	多層スパースモデル (MLSTD)
学習可能なフィルタ	最適化アルゴリズムを展開し，フィルタ係数を学習	フィルタリングした信号がスパース	深層展開 (DU)

データに内在する構造は，必ずしも元の表現で最も扱いやすいとは限りません．適切な変換を施すことで，その本質的なスパース性を引き出し，より高度な信号処理や機械学習モデルを構築することが可能になります．今後，深層展開との融合により，データから最適な変換そのものを学習する研究がさらに進展していくことが期待されます．

参考文献

より深い技術的詳細に関心のある方は，以下の論文をご参照ください．

■ ブロックスパース正則化を用いた画像平滑化（手前味噌😚）
[1] T. Furuhashi, H. Hontani, and T. Yokota, “Adaptive Block Sparse Regularization Under Arbitrary Linear Transform,” in Proceedings of European Signal Processing Conference, Aug. 2024, pp. 2437–2441. doi: 10.23919/EUSIPCO63174.2024.10714986.

■ ブロックスパース正則化を用いた周波数帯域選択
[2] H. Kuroda and D. Kitahara, “Block-sparse recovery with optimal block partition,” IEEE Transactions on Signal Processing, vol. 70, pp. 1506–1520, 2022, doi: 10.1109/TSP.2022.3156283.

■ 多層スパース性を用いたテンソル補完
[3] J. Xue, Y. Zhao, S. Huang, W. Liao, J. C.-W. Chan, and S. G. Kong, “Multilayer Sparsity-Based Tensor Decomposition for Low-Rank Tensor Completion,” IEEE Trans. Neural Netw. Learning Syst., vol. 33, no. 11, pp. 6916–6930, Nov. 2022, doi: 10.1109/TNNLS.2021.3083931.

■ 平滑低ランクモデルを用いたテンソル復元
[4] H. Wang, J. Peng, W. Qin, J. Wang, and D. Meng, “Guaranteed Tensor Recovery Fused Low-rankness and Smoothness,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, no. 9, pp. 10990–11007, Sep. 2023, doi: 10.1109/TPAMI.2023.3259640.

■ 行列の特異値・核ノルムに関する数学的背景の解説
[5] Strang G. and 松崎公紀, ストラング : 線形代数とデータサイエンス. 近代科学社, 2021. Accessed: Jul. 18, 2022. [Online]. Available: https://ci.nii.ac.jp/ncid/BC10710871

■ 高階テンソル（多次元配列）に対する核ノルムの数学的背景
[6] W. Qin, H. Wang, F. Zhang, J. Wang, X. Luo, and T. Huang, “Low-Rank High-Order Tensor Completion With Applications in Visual Data,” IEEE Transactions on Image Processing, vol. 31, pp. 2433–2448, 2022, doi: 10.1109/TIP.2022.3155949.

■ 深層展開による学習可能なフィルタを用いた時変グラフ信号の復元
[7] H. Kojima, H. Noguchi, K. Yamada, and Y. Tanaka, “Restoration of Time-Varying Graph Signals using Deep Algorithm Unrolling,” in ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Jun. 2023, pp. 1–5. doi: 10.1109/ICASSP49357.2023.10094838.

■ 深層展開の基礎や収束解析に関する日本語解説
[8] Wadayama T. and Takabe S., “Deep Unfolding Approach for Signal Processing Algorithms: Convergence Acceleration and Its Theoretical Interpretation,” Fundamentals Review, vol. 14, no. 1, pp. 60–72, Jul. 2020, doi: 10.1587/essfr.14.1_60.

■ 深層展開のサーベイ論文．近接勾配法やADMMなどの最適化アルゴリズムを深層展開する方法も扱っている
[9] V. Monga, Y. Li, and Y. C. Eldar, “Algorithm Unrolling: Interpretable, Efficient Deep Learning for Signal and Image Processing,” IEEE Signal Process. Mag., vol. 38, no. 2, pp. 18–44, Mar. 2021, doi: 10.1109/MSP.2020.3016905.

Takanobu Furuhashi

Explorer

特徴空間におけるスパース正則化：潜在的なスパース性の抽出